Eine neue Studie zeigt, dass die jahrhundertealten Formeln von Srinivasa Ramanujan zur Berechnung von Pi unerwartet in modernen Theorien kritischer Phänomene, Turbulenzen und schwarzer Löcher auftauchen.
In der Schule begegnen viele von uns zum ersten Mal der irrationalen Zahl π (Pi) – gerundet als 3,14, mit einer unendlichen Anzahl von Dezimalstellen – wenn wir lernen, wie der Umfang eines Kreises mit seinem Durchmesser zusammenhängt. Seitdem hat die Rechenleistung enorm zugenommen, und moderne Supercomputer können jetzt Billionen von Stellen dieser Konstante berechnen.
Forscher des Centrums für Hochenergiephysik (CHEP) am Indian Institute of Science (IISc) haben nun gezeigt, dass einige der rein mathematischen Formeln, die vor einem Jahrhundert zur Berechnung von Pi entwickelt wurden, eng mit der fundamentalen Physik von heute verbunden sind. Diese alten Formeln treten in theoretischen Modellen wieder auf, die zur Untersuchung von Perkolation, Turbulenz und bestimmten Aspekten schwarzer Löcher verwendet werden.
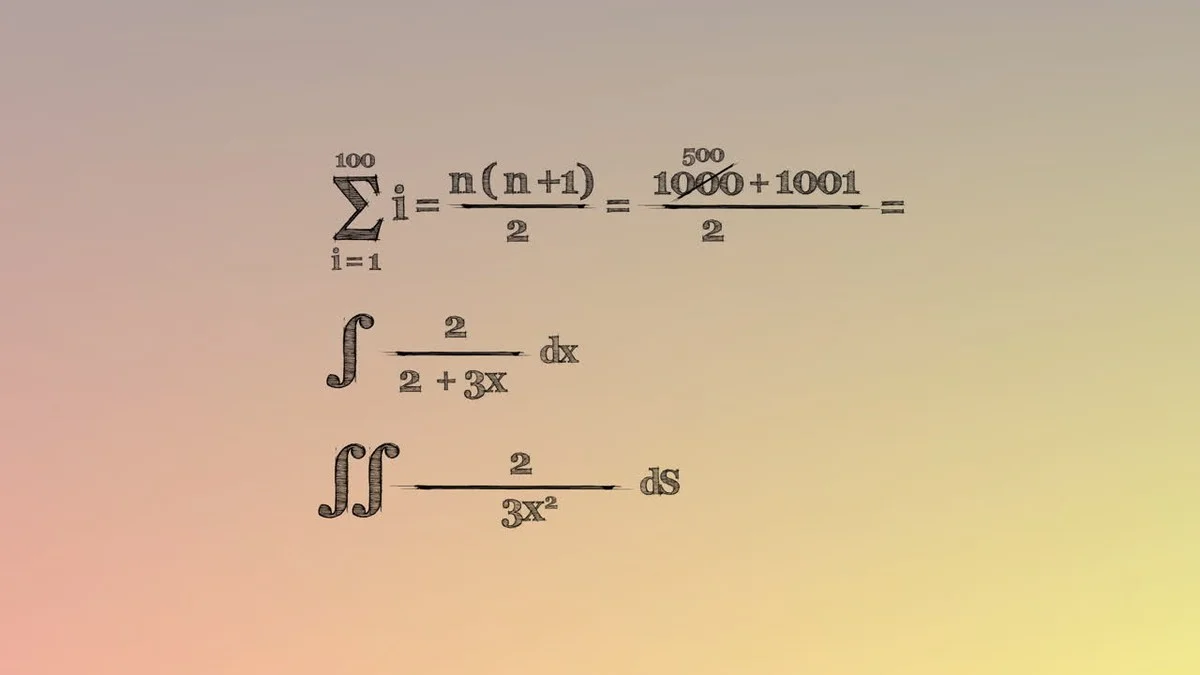
Ein Blick zurück: Ramanujans Beitrag zur Mathematik
Der Weg führt zurück ins Jahr 1914. Kurz bevor er Madras nach Cambridge verließ, veröffentlichte der berühmte indische Mathematiker Srinivasa Ramanujan eine Arbeit, die 17 Formeln zur Berechnung von Pi einführte. Diese Formeln waren außergewöhnlich effizient und ermöglichten eine schnellere Berechnung von Pi als mit anderen damals verfügbaren Methoden. Obwohl sie nur eine geringe Anzahl von mathematischen Termen enthielten, lieferten sie dennoch viele korrekte Dezimalstellen von Pi. Im Laufe der Jahre wurden sie so wichtig, dass sie heute moderne rechnerische und mathematische Techniken zur Auswertung von Pi untermauern, einschließlich der Methoden, die auf heutigen Supercomputern verwendet werden.
„Wissenschaftler haben Pi bis zu 200 Billionen Stellen unter Verwendung eines Algorithmus namens Chudnovsky-Algorithmus berechnet“, sagt Aninda Sinha, Professor am CHEP und Co-Autor der neuen Studie. „Diese Algorithmen basieren tatsächlich auf Ramanujans Arbeiten.“
Die tiefere Frage: Warum existieren diese Formeln?
Die Frage, die Sinha und Faizan Bhat, erster Autor und ehemaliger Doktorand am IISc, stellten, lautete: Warum sollten solch erstaunliche Formeln überhaupt existieren? In ihrer Arbeit suchten sie nach einer physikalischen Antwort. „Wir wollten sehen, ob der Ausgangspunkt seiner Formeln natürlich in irgendeiner Physik verankert ist“, erklärt Sinha. „Anders ausgedrückt, gibt es eine physikalische Welt, in der Ramanujans Mathematik von selbst erscheint?“
Sie entdeckten, dass Ramanujans Formeln natürlicherweise innerhalb einer breiten Klasse von Theorien auftauchen, die als konforme Feldtheorien bekannt sind, insbesondere innerhalb von logarithmischen konformen Feldtheorien. Konforme Feldtheorien beschreiben Systeme mit Skaleninvarianzsymmetrie – im Wesentlichen Systeme, die unabhängig davon identisch erscheinen, wie tief man hineinzoomt, ähnlich wie Fraktale. Im physikalischen Kontext kann dies am kritischen Punkt von Wasser gesehen werden, einer besonderen Temperatur und einem besonderen Druck, bei denen die flüssigen und dampfförmigen Formen von Wasser nicht mehr unterscheidbar sind.

An diesem Punkt zeigt Wasser eine Skaleninvarianzsymmetrie, und seine Eigenschaften können mit Hilfe der konformen Feldtheorie beschrieben werden. Kritisches Verhalten tritt auch bei der Perkolation (wie sich Dinge durch ein Medium verbreiten), beim Übergang zur Turbulenz in Flüssigkeiten und in bestimmten Beschreibungen schwarzer Löcher auf – Phänomene, die durch die spezifischeren logarithmischen konformen Feldtheorien erklärt werden können.
Ramanujans Mathematik in der Physik
Die Forscher fanden heraus, dass die mathematische Struktur, die dem Ausgangspunkt von Ramanujans Formeln zugrunde liegt, auch in den mathematischen Grundlagen dieser logarithmischen konformen Feldtheorien vorkommt. Mit dieser Verbindung konnten sie bestimmte Größen in diesen Theorien effizient berechnen – Größen, die potenziell helfen könnten, Phänomene wie Turbulenz oder Perkolation besser zu verstehen. Dies ähnelt dem Prozess von Ramanujan, der vom Ausgangspunkt seiner Formeln aus Pi effizient ableitete. „In jedem Stück schöner Mathematik findet man fast immer ein physikalisches System, das die Mathematik widerspiegelt“, sagt Bhat. „Ramanujans Motivation mag sehr mathematisch gewesen sein, aber ohne sein Wissen hat er auch schwarze Löcher, Turbulenzen und Perkolation studiert.“
Die Studie zeigt, dass Ramanujans jahrhundertealte Formeln eine bislang verborgene Anwendung in der Beschleunigung aktueller Berechnungen der Hochenergiephysik haben. Auch ohne diese Entdeckung sind Sinha und Bhat von der Schönheit von Ramanujans Mathematik fasziniert. „Wir waren einfach begeistert davon, wie ein Genie, das zu Beginn des 20. Jahrhunderts in Indien arbeitete und kaum Kontakt zur modernen Physik hatte, Strukturen anticipierte, die nun zentral für unser Verständnis des Universums sind“, sagt Sinha.









